In our Big Story in bl.portfolio dated March 3, 2024, we explained how statistical measures, including mean, standard deviation, beta, alpha, and correlation, can be used to make informed investment decisions. However, you would have noticed that successful investors often emphasise risk management as a crucial component of investing because it helps protect their capital from significant losses and ensures long-term sustainability. So, here we present five statistical tools to assess the risks in your portfolio and manage them well.
Coefficient of Variation
By comparing the volatility (represented by the standard deviation of returns) to the average return, the coefficient of variation (CV) provides an assessment of the risk-return relationship inherent in investment decisions. Standard deviation quantifies the extent to which a stock’s price tends to deviate from its average return and can be computed using Excel. A lower CV signifies less dispersion around the average return, indicating lower risk per unit of average return. This metric enables investors to gauge the level of risk relative to the asset’s returns.
While this tool can be applied to an individual’s stock portfolio, it is applicable even if you are a mutual fund investor. Let us take the example of a flexi-cap fund, Fund A, which has a five-star rating in our bl.portfolio Star Track Ratings. One way for an investor to analyse its risk-adjusted returns is by applying a CV. Comparing the fund’s three-year performance against the fund’s benchmark S&P BSE 500 TRI, it’s evident that the fund has outperformed its benchmark. Additionally, the fund exhibits a CV of 0.49, while the benchmark’s CV stands at 0.69. This comparison underscores the relatively lower risk associated with the fund’s returns.
While the CV is an effective and simple way to assess risk-adjusted returns, it encounters limitations when applied to portfolios that have experienced periods of negative returns as the ratio may not provide meaningful insights in such instances. Alternative risk-adjusted measures such as the Sharpe and Sortino ratios can be useful here.
Sharpe and Sortino Ratios
While the Sharpe ratio can be used to assess any portfolio, in India it is well known for measuring risk-adjusted returns in mutual funds. This ratio evaluates how much extra return a fund generates over the risk-free rate per unit of risk. To compute the Sharpe Ratio, we subtract the risk-free rate (often represented by the overnight MIBOR rate) from the fund’s average return and then divide it by the standard deviation of the fund’s returns.
A higher Sharpe Ratio indicates that the fund is adept at generating higher returns for the level of risk taken. A negative Sharpe ratio, on the other hand, indicates that the fund has delivered a return that doesn’t compensate investors for the level of risk they’ve assumed. That said, the standard deviation in the Sharpe Ratio includes both upside and downside deviation, whereas investors are mainly concerned about downside risk.
For this reason, investors can turn to the Sortino ratio, which focuses solely on downside deviation risk, especially for those prioritising downside protection. It employs the same formula as the Sharpe ratio but considers only the downside standard deviation. While these ratios need to be manually computed if you want to make these assessments for your portfolio, in the case of mutual funds, it is readily available in fund factsheets and online resources such as BL.Portfolio Mutual Funds ratings,Morningstar, and Value Research online.
Let’s understand by considering two small-cap funds B and C, which have delivered similar 3-year CAGR trailing returns of around 27 per cent. Their Sortino ratios differ, with Fund B exhibiting a ratio of 0.5 and Fund C at 0.45, as per the Bl.portfolio Star Track Ratings. The higher Sortino ratio of Fund B indicates that it has generated superior downside risk-adjusted returns compared to Fund C, despite their similar overall returns.
Skewness and Kurtosis
Generally, it’s assumed that data distributions, such as stock returns, tend to approximate to normal distribution over a large period of time, adhering to the symmetrical bell-shaped curve pattern (the statistical concept called the Central Limit Theorem). However, there could be deviations from this norm, influenced by factors such as market dynamics, information asymmetry, risk factors, occurrences of extreme events, and investors’ behavioural biases. Metrics such as skewness and Kurtosis come in here.
Skewness serves as a quantitative tool to find out the direction and magnitude of deviations from the average returns. For instance, a negatively skewed distribution (skewness less than zero), indicates a propensity for frequent small gains alongside occasional extreme losses, thereby signalling potential downside risk. On the other hand, a positively skewed distribution (skewness greater than zero), suggests a higher probability of small losses juxtaposed with sporadic extreme gains. However, if an asset’s return distribution exhibits a symmetric pattern (bell curve), then there will be no skewness.

Kurtosis adds another layer of insight by quantifying the peakedness or flatness of a distribution relative to a normal distribution. When the return data follows a bell-shaped curve, the value of kurtosis (or excess kurtosis) is equal to three (or zero). High kurtosis values, exceeding three (positive excess kurtosis), indicate a heightened frequency of outliers or extreme events that can exert a significant influence on returns. Conversely, kurtosis values below three (negative excess kurtosis) suggest a flatter distribution, indicating a reduced likelihood of extreme deviations from the average return. In general, positive excess kurtosis and more negative skew in return distributions indicate increased risks.
Spreadsheet software can readily calculate these measures. However, it’s important to note that Excel computes excess kurtosis which is equal to the value of kurtosis minus three.
Here is how skewness and kurtosis can be applied to investing using examples of the patterns in the various sectoral indices. Nifty FMCG exhibits positive skewness and low excess kurtosis, aligning with the sector’s non-cyclical/defensive investment nature. Consequently, FMCG stocks may appeal to conservative investors seeking steady, modest returns amid market volatility. Nifty Healthcare, on the other hand, displays positive skewness alongside high kurtosis, suggesting a sector with a higher propensity for abnormal positive returns.
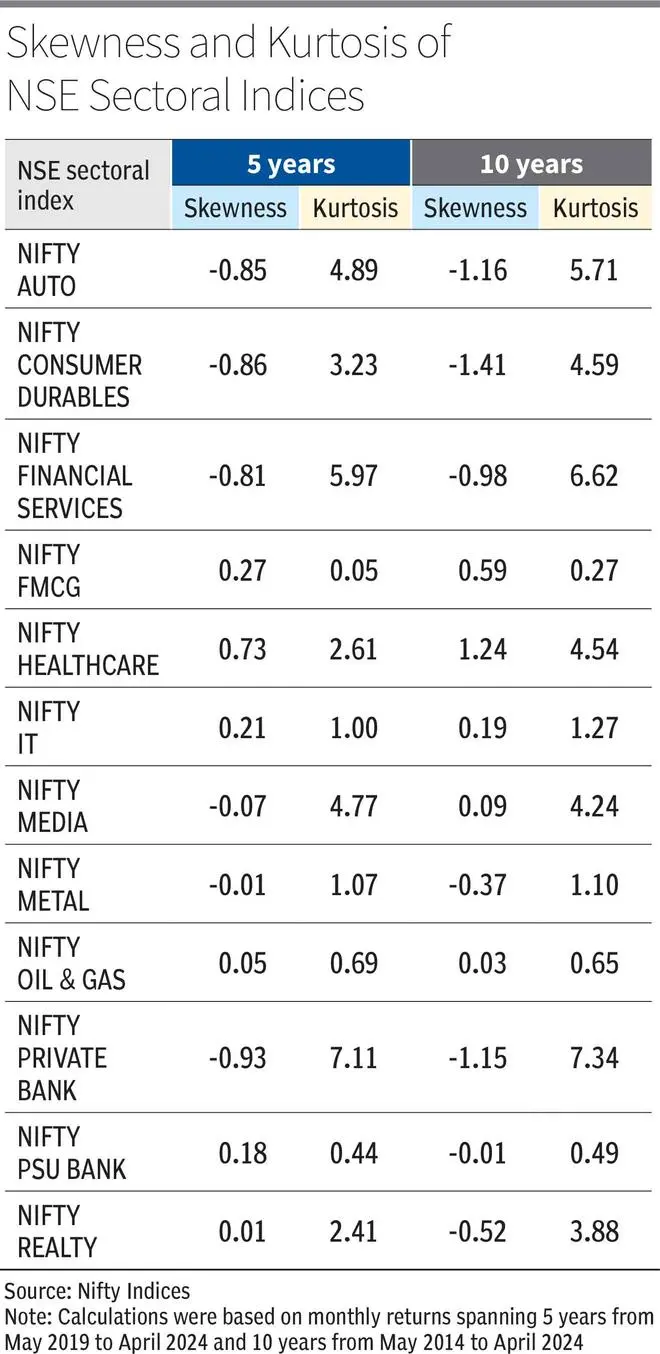
In contrast, sectors such as Nifty Auto, Nifty Consumer Durables, and Nifty Private Bank demonstrate high negative skewness and positive excess kurtosis. This implies a higher likelihood of extreme negative returns, making these sectors more susceptible to higher risk and market fluctuations. For instance, the automotive and consumer durables sectors are sensitive to economic cycles and consumer spending patterns, while the banking sector faces regulatory, economic, and market risks. Consequently, investors with higher risk tolerance levels may find these sectors appealing, but they should also factor in the potential for significant downside risk.
Expanding the scope beyond equity investments, conservative investors may find gold to be an attractive asset class. With positive skewness (0.41), and low excess kurtosis (0.13) over the last 10 years, gold prices tend to show more moderate gains than losses, with fewer extreme price movements compared to other assets. This stability makes gold a potential hedge against inflation and geopolitical uncertainty, enhancing diversification in conservative portfolios. By incorporating assets with diverse skewness and kurtosis characteristics, investors can mitigate overall portfolio risk and enhance the potential for stable, risk-adjusted returns.
Value at Risk
Value at Risk (VaR) is applicable across diverse financial instruments, spanning stocks, bonds, and derivatives. It gauges the potential downside of an investment portfolio, estimating the minimum loss likely to occur within a specified time period with a given probability. While retail investors can benefit from VaR, its primary users encompass financial institutions, portfolio managers, and institutional investors, utilising it to evaluate and mitigate investment risks at a portfolio level.
Though manual computation of VaR can be complex, investors can make use of the VaR margin available in stock exchanges. For instance, consider a sample portfolio comprising 2 shares of Maruti Suzuki, 6 shares of TCS, 12 shares of HUL, and 16 shares of HDFC Bank, with a notional value of around ₹1 lakh (around ₹25,000 in each company). By inputting these values in the NSE margin calculator, one can see that the daily VaR of this sample portfolio amounts to around ₹8,999.5 as of May 2. It should be noted that the VaR margin in these exchanges is updated at regular time intervals throughout the trading day to reflect market movements.
Typically, monitoring a portfolio’s VaR at predefined intervals is crucial. If it increases due to market turbulence, it signals the need to potentially adjust positions or mitigate risk by diversifying the holdings.
However, VaR has its own set of constraints. Its reliance on historical data and statistical models may occasionally make it falter in predicting future market movements, particularly during extreme volatility or unforeseen events. Moreover, VaR may not encapsulate all risk facets, such as liquidity or event risks, which could sway portfolio performance. Additionally, VaR’s reliability hinges on the accuracy of data and assumptions underlying its computation, necessitating investors to supplement it with strategies such as sensitivity analysis and scenario analysis.





Comments
Comments have to be in English, and in full sentences. They cannot be abusive or personal. Please abide by our community guidelines for posting your comments.
We have migrated to a new commenting platform. If you are already a registered user of TheHindu Businessline and logged in, you may continue to engage with our articles. If you do not have an account please register and login to post comments. Users can access their older comments by logging into their accounts on Vuukle.